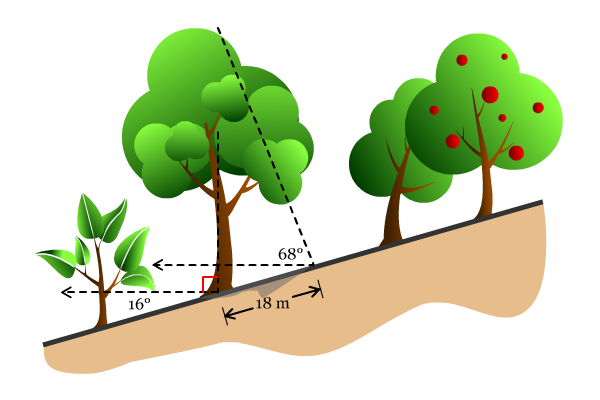
Sebuah pohon tumbuh secara vertikal pada daerah pegunungan. Permukaan tanah dari daerah pegunungan tersebut memiliki kemiringan 16° terhadap garis horizontal. Apabila panjang bayangan pohon tersebut adalah 18 meter ketika besar sudut elevasi yang dihasilkan oleh sinar matahari sebesar 68°, tentukan tinggi dari pohon tersebut?
Pembahasan
Misalkan α adalah sudut lancip yang dibentuk oleh pohon dan permukaan tanah, maka:
Misalkan β adalah sudut lancip yang dibentuk oleh sinar matahari dengan permukaan tanah, maka:
Semoga Bermanfaat.....

Pembahasan
Misalkan α adalah sudut lancip yang dibentuk oleh pohon dan permukaan tanah, maka:
α + 90° + 16° = 180°Sehingga diperoleh α = (180 – 90 – 16)° = 74°.
Misalkan β adalah sudut lancip yang dibentuk oleh sinar matahari dengan permukaan tanah, maka:
β = (68 + 16)° = 84°Sudut-sudut α dan β merupakan sudut-sudut dalam segitiga. Selanjuntya kita tentukan besar sudut dalam segitiga yang lainnya, misalkan θ, yaitu sudut yang dibentuk oleh pohon dengan sinar matahari. Untuk menentukan besar θ, kita gunakan sifat jumlah sudut dalam segitiga.
α + β + θ = 180°Sehingga diperoleh θ = (180 – 74 – 84)° = 22°. Setelah itu kita tentukan tinggi pohon, misalkan t, dengan menggunakan aturan sinus: (sin β) / t = (sin θ) / 18. Diperoleh, t = (18 ∙ sin β) / sin θ = (18 ∙ sin 84°) / sin 22° ≈ 47,79. Jadi, tinggi pohon tersebut adalah sekitar 47,79 meter.
Semoga Bermanfaat.....
 RSS Feed
RSS Feed Twitter
Twitter 01.00
01.00
 Ayo Berbagi
Ayo Berbagi
 Posted in
Posted in
0 komentar:
Posting Komentar